Characteristic |
Beta |
95% CI 1 |
|---|---|---|
| age | -0.04 | -0.05, -0.04 |
| sex | ||
| Male | — | — |
| Female | 0.18 | 0.13, 0.23 |
| episode_number | -0.03 | -0.06, 0.00 |
| 1
CI = Credible Interval |
||
Model
To model the effects of different variables on the probability of survival, we used the following equation…
\[ \text{logit}(\pi_i) = \beta_0 + \beta_1 \cdot \text{age}_i + \beta_2 \cdot \text{sex}_{i,\text{Male}} + \beta_3 \cdot \text{episode\_number}_i \]
We recieve the following results indicating a positive effect on the probability of survival if one is female, while there is a decrease in the probability if one is of older age or has more episode numbers…
To visually interpret the survival probability, the model is graphed by taking draws and using the average age of patients.
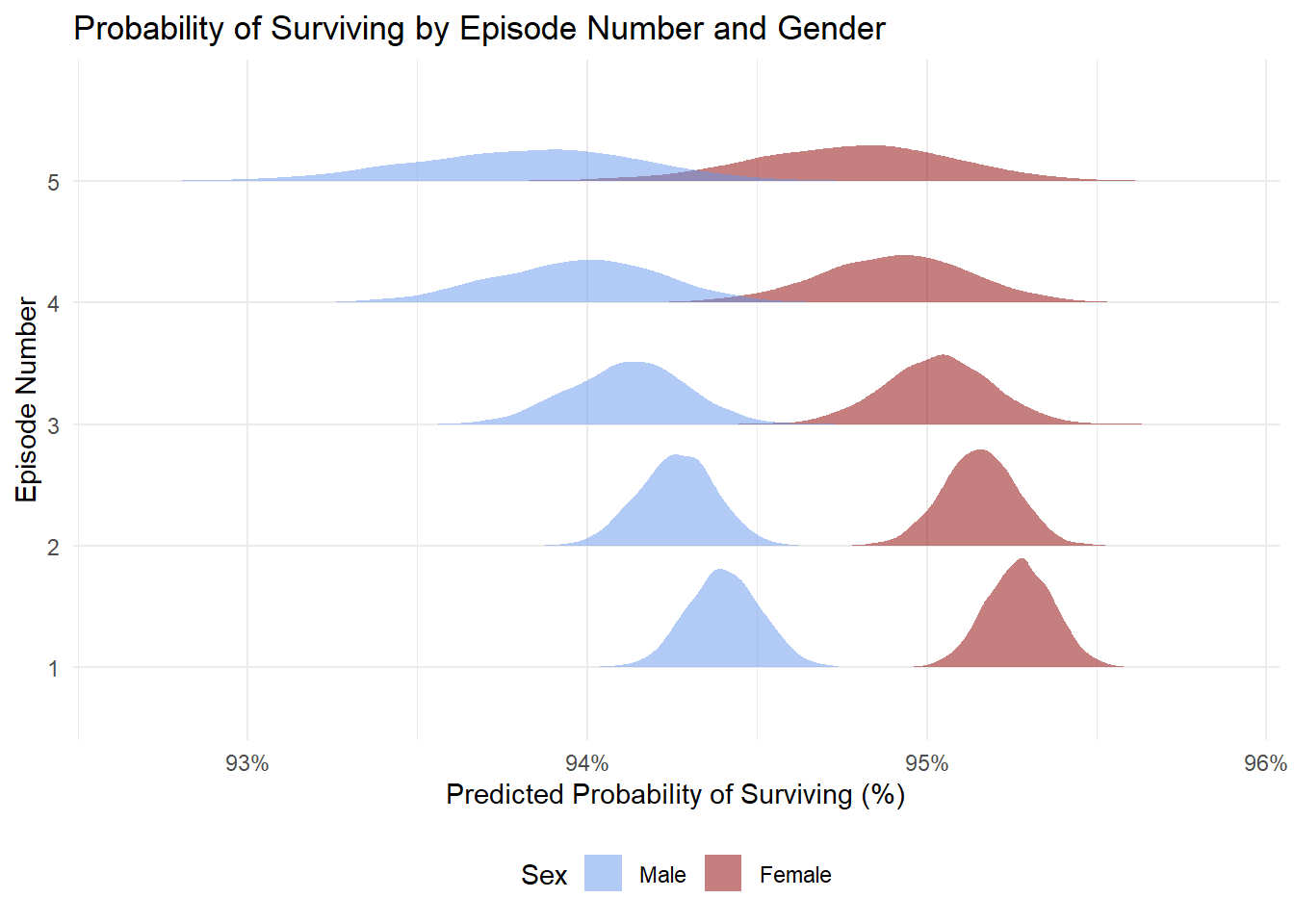
From this we see that females of younger age with less episode numbers have the highest likelihood of survival while males of older age with more episode numbers would have the lowest likelihood of survival.
Predict Your Own Survival Probability
To model one’s own probability of survival, one can input their variables into the equation using the numbers from the table.
Example for a female with 1 episode of Sepsis of 50 years of age:
We take the equation:
\[ \text{log-odds} = \beta_0 + \beta_1 \cdot \text{age} + \beta_2 \cdot \text{sexFemale} + \beta_3 \cdot \text{episode\_number} \]
Where:
\[\begin{align*} \beta_0 \, (\text{Intercept}) &= 5.63 \\ \beta_1 \, (\text{age}) &= -0.044 \\ \beta_2 \, (\text{sexFemale}) &= 0.178 \\ \beta_3 \, (\text{episode\_number}) &= -0.025 \\ \end{align*}\]
We input the values in the table and variables of each individual into the equation:
\[\text{log-odds} = 5.63 + (-0.044 \cdot 50) + (0.178 \cdot 1) + (-0.025 \cdot 1)\] After calculation, the resulting probability is 97.3%
This can be done for all individuals, though note that this is only a prediction.